Sine cosine graphs
Table of Contents
Table of Contents
If you’re struggling with drawing sine and cosine graphs, you’re not alone. It can be a challenging concept to grasp, but once you understand it, it can open up a world of possibilities in the field of math. In this blog post, we’ll go through how to draw sine and cosine graphs, step-by-step.
When it comes to drawing sine and cosine graphs, it can be difficult to know where to start. Some common pain points include not knowing how to interpret the equations, and struggling to understand the relationship between the graphs and the unit circle. But don’t worry, once you understand the basics, it becomes much easier.
The first thing to know when it comes to drawing sine and cosine graphs is that they are periodic functions. This means that they repeat themselves over and over again. The period of a sine or cosine graph is defined by the coefficient in front of the x in the equation. For example, the period of y = sin(2x) is π, while the period of y = cos(3x) is 2π/3.
To draw a sine or cosine graph, start by plotting the x-intercepts (or zeros) on the x-axis. Then, plot the maximum and minimum points (or the amplitude) of the graph. The maximum and minimum points will be determined by the coefficient in front of the sine or cosine function. Once you’ve plotted these points, you can connect them with smooth, curved lines to create the graph.
In summary, to draw a sine or cosine graph, you first need to understand the period and amplitude of the function. Then plot the x-intercepts and the maximum and minimum points, and connect them with smooth, curved lines to create the graph.
Understanding the Period and Amplitude of Sine and Cosine Graphs
When it comes to drawing sine and cosine graphs, it’s important to understand the period and amplitude of the function. The period of a sine or cosine function is the length of one complete cycle of the function. The amplitude is the distance between the horizontal midline and the maximum or minimum of the function.
For example, in the function y = 2sin(3x), the period is 2π/3 and the amplitude is 2.

Graphing Sine and Cosine Functions Using the Unit Circle
The unit circle is a powerful tool for understanding trigonometric functions, and it can be used to help graph sine and cosine functions. When you graph a sine or cosine function using the unit circle, you start by placing a point on the unit circle corresponding to the given angle. Then, you draw a line from the origin to the point on the unit circle, which gives you the x and y coordinates of the point.
 Once you have the x and y coordinates, you plot them on the coordinate plane, which gives you a point on the sine or cosine graph. Repeat this process for various angles to create the entire graph.
Once you have the x and y coordinates, you plot them on the coordinate plane, which gives you a point on the sine or cosine graph. Repeat this process for various angles to create the entire graph.
Using Technology to Graph Sine and Cosine Functions
While it’s important to understand the mechanics of graphing sine and cosine functions by hand, there are also many tools available to make the process easier. For example, graphing calculators and software like Desmos can quickly and accurately graph complex functions.
One benefit of using technology to graph sine and cosine functions is that you can easily adjust the coefficients of the function to see how they affect the graph. This can help deepen your understanding of the relationships between the equations and the resulting graphs.
Using Sine and Cosine Graphs in Real Life
Sine and cosine functions are not just abstract mathematical concepts. They can be used to model and understand many real-world phenomena, such as sound waves and light waves. By understanding the properties of sine and cosine functions, you can gain insights into the behavior of these waves, which can have practical applications in fields like physics and engineering.
Frequently Asked Questions
Q: What is the difference between the graphs of sine and cosine functions?
A: Sine and cosine functions are both periodic functions that repeat themselves over and over again. The difference between the two is that the sine function starts at 0, while the cosine function starts at 1.
Q: How can I remember the period and amplitude of trigonometric functions?
A: One trick is to use the acronym SOHCAHTOA. This stands for “Sine is Opposite over Hypotenuse, Cosine is Adjacent over Hypotenuse, and Tangent is Opposite over Adjacent.” This can help you remember the basic properties of these functions.
Q: What are some practical applications of sine and cosine functions?
A: Sine and cosine functions are used in many fields, including physics, engineering, and even music. For example, they can be used to model sound waves and light waves, and to understand the behavior of electrical circuits.
Q: How can I check my work when graphing a sine or cosine function?
A: One way to check your work is to use a graphing calculator or software like Desmos to compare your graph to the computer-generated graph. Another way is to check that your function satisfies the basic properties of sine and cosine functions, such as being periodic and having a maximum and minimum.
Conclusion of How to Draw Sine and Cosine Graphs
Drawing sine and cosine graphs can be a challenging concept to grasp, but with practice and patience, you can become an expert in no time. Remember to understand the period and amplitude of the functions, and to use tools like the unit circle and graphing calculators to make the process easier. By mastering sine and cosine functions, you can gain a deeper understanding of the world around you and its mathematical properties.
Gallery
Practice On Problem Solving: Graph Of Sine And Cosine Function.
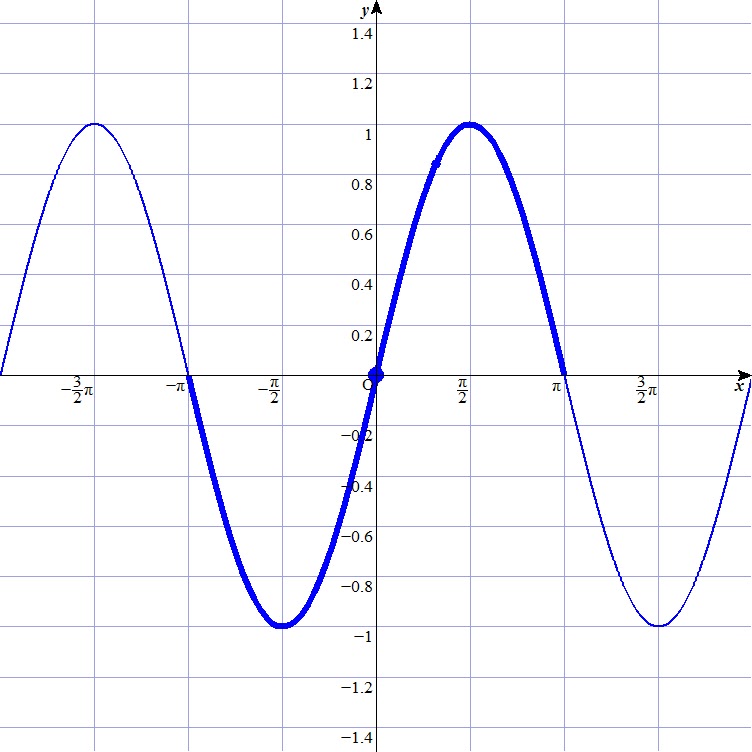
Photo Credit by: bing.com / graph sine sin cosine function value problem solving practice blue red
Trigonometry On The New SAT

Photo Credit by: bing.com / trigonometry sat cosine sine
Sine Graphs Worksheet
Photo Credit by: bing.com / sine graphs mathsisfun cosine trigonometry math
L3inary

Photo Credit by: bing.com / functions sin cos cosine sine find circle tool unit learn trigonometric
4-06 Graphs Of Sine And Cosine
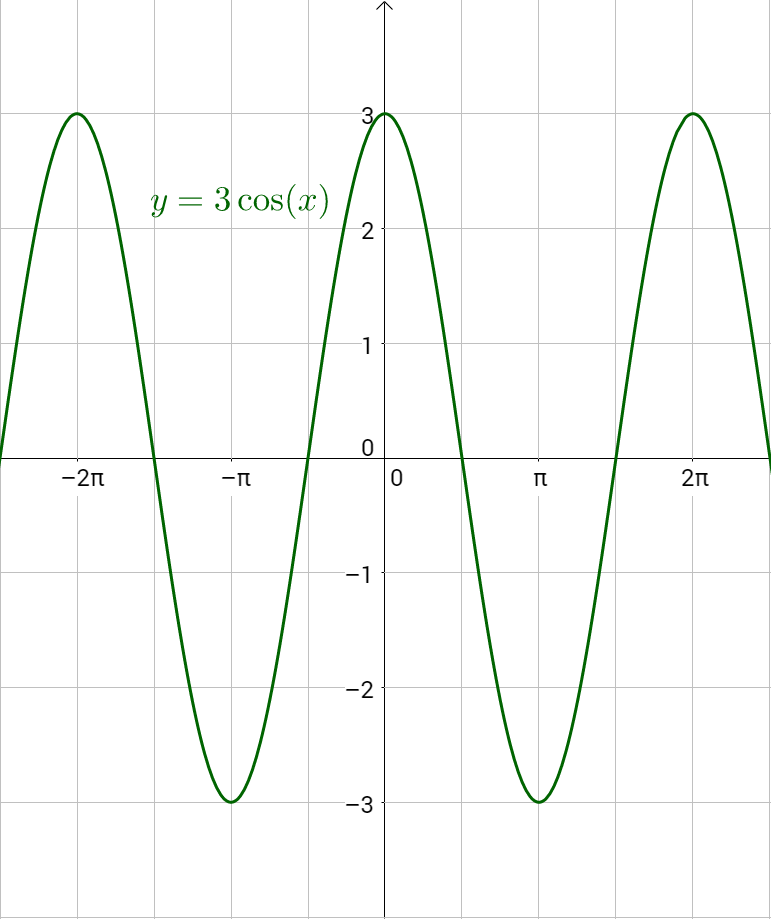
Photo Credit by: bing.com / sine cosine graphs